I hope the last article was easy enough and well explained on differentiation. If any problem
or unclear though anyone have please let me know.
Let us start with the partial derivative.
If a function f(x) has multiple variables in it like f(x,y,z,w,p) = 5xy+z+wp, then we define
partial derivatives (derivatives and differentiation are one and the same thing)
Partial derivative is nothing but the differentiation of the function with respect to only one
variable, keeping rest of the variables as constant. It is denoted by
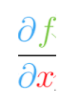
For example, we can take the partial derivative of above function with respect to w:
d(f)/d(w) = d(5xy)/dw +dz/dw + d(wp)/dw
treating rest all variables as constant, our derivative will be
d(f)/d(w) = 0 + 0 + p* d(w)/dw (applying the derivative rule for constant, derivative of a
constant is 0)
hence, df/dw = p
I hope it is clear, if not please let me know.
Let’s calculate the intercept and slope of linear regression model with the help of partial
differentiation.
In the case of simple linear regression, the independent variable is only one as it x and only
one response variable say Y. Let us assume that the true relationship between Y and x is a
straight line (if you remember y = slope*x + intercept) and the observation Y for each level
of x is a random variable, as we all know that the expected value of Y for each value of x
is:
E(Y|x) = β0 + β1 * x
Where the intercept β0 and slope β1 are the unknow regression coefficient.
There is an assumption that each observation can be described by the equation:
Y = β0 + β1 * x + ε
Where ε is random error with mean zero and (Unknown) Variance σ2.
Suppose that we have n pairs of observations (x1, y1), (x2, y2 ),…, (xn, yn ).
The estimates of β0 and β1 should result in a line that is (in some sense) a “best fit” to the
data. The German scientist Karl Gauss (1777–1855) proposed estimating the parameters β0
and β1 to minimize the sum of the squares of the vertical deviations which is the error ε.
We call this criterion for estimating the regression coefficients the method of least
squares. we may express the n observations in the sample as
yi = β0 + β1 * xi + εi Where I = 1,2,3…..n are the different observations.
Hence, keeping the error on one side,
εi = (yi – β0 – β1 * xi)
as the method is least square method, Hence, we have to square it:

in more extended form:

To calculate overall sum of squared error, we have to sum all these errors:
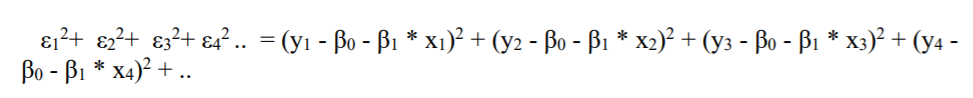
Mathematically it is denoted by:
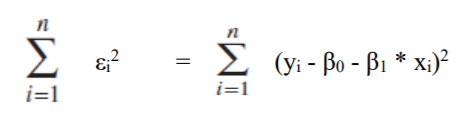
Let us denote it by L.
Hence,
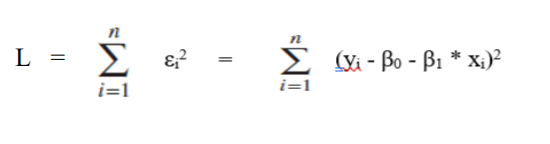

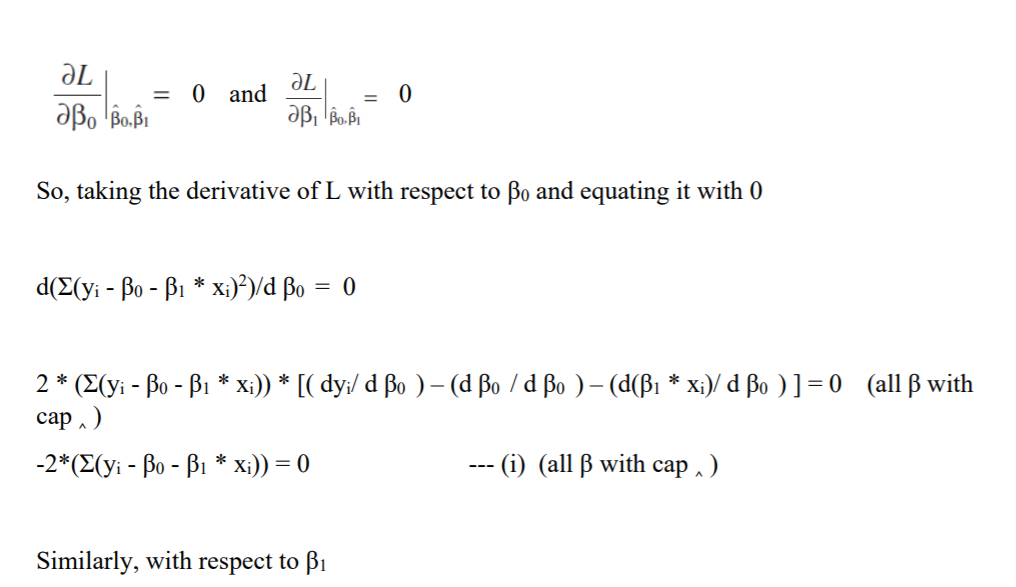
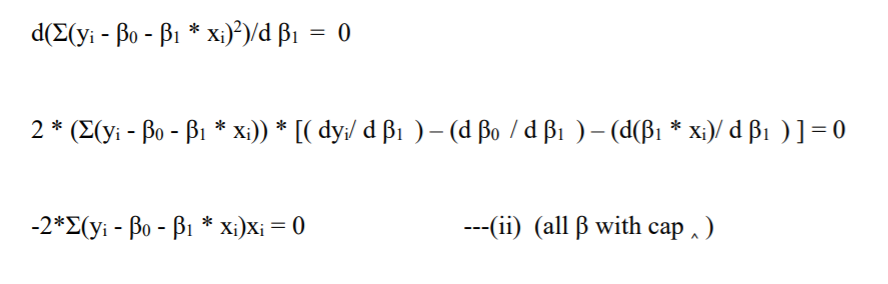
Solving equation (i) and equation (ii),
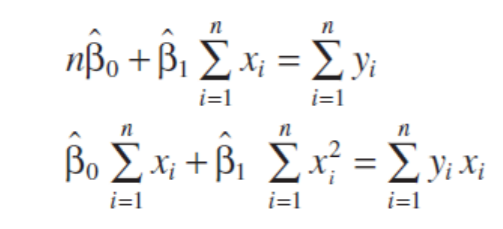

This is how, we calculate the intercept and slope of the simple linear regression.
I would suggest to practice this derivation and also use the moment generating function to
calculate the Expected value and Variance.
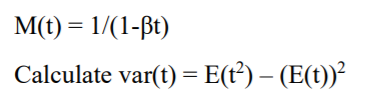
I will explain the Linear algebra and Vectors in next article.
Reference: Applied Statistics and Probability for Engineers by Douglas C. Montgomery,
George C. Runger
