
Time series analysis helps to solve business problems which are time-based and identify this timebased pattern in the future. Techniques of time series forecasting could answer business questions like how much inventory to maintain, what will be sales for next month, what will be the demand of products, what will be the website traffic in the e-store and likewise. The basic objective of time series analysis usually is to determine a model that describes the pattern of the time series data which can help in forecasting the data.
A time series is modeled through a stochastic process Y(t), i.e a sequence of random variables. In a forecasting setting we find ourselves at time t and we are interested in estimating Y(t+h), using only information available at time t.
One of the traditional methods to forecast the time series data is through ARIMA model. I have posted an article on ARIMA model. One can find the details and python implementation of the ARIMA method in my previous post on LinkedIn.
In this article, I will be talking about FB Prophet, an open sourcing forecasting tool developed by Facebook Inc. This method takes two input from data set. The date stamp, which is abbreviated as ‘ds’ and the dependent variable ‘y’, which need to be forecasted. This article provides you details about FB Prophet, and a comparison between FB Prophet and ARIMA model output.
For the analysis purpose, I have taken Walmart sales dataset from Kaggle. For the ease of model, I have selected store-1 and department- 1.
Link of the data set: https://www.kaggle.com/iamprateek/wallmart-sales-forecast-datasets
How FB Prophet works?
At its core, the Prophet procedure is an additive regression model with four main components:
• A piecewise linear or logistic growth curve trend. Prophet automatically detects changes
in trends by selecting changepoints from the data.
• A yearly seasonal component modeled using Fourier series.
• A weekly seasonal component using dummy variables.
• A user-provided list of important holidays.
The Prophet uses a decomposable time series model with three main model components: Trend, Seasonality, and Holidays. It combines and form equation as mentioned below:
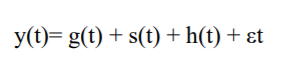
• g(t): piecewise linear or logistic growth curve for modeling non-periodic changes in time
series
• s(t): periodic changes (e.g. weekly/yearly seasonality)
• h(t): effects of holidays (user provided) with irregular schedules
• εt: error term accounts for any unusual changes not accommodated by the model
Using time as a regressor, Prophet is trying to fit several linear and non-linear functions of time as components. Prophet frames the forecasting problem as a curve-fitting exercise rather than looking explicitly at the time-based dependence of each observation within a time-series.
Validation of data is like any other time-series forecasting. Due to the temporal dependencies in time series data, we ensure that training set contains observations that occurred prior to the ones in validation sets.
To evaluate the performance of the model, I have used sMAPE (Symmetric mean absolute
percentage error) criteria. sMAPE is the error evaluated between forecasted and actual values.
Let’s code for FB Prophet:
Importing the required libraries:
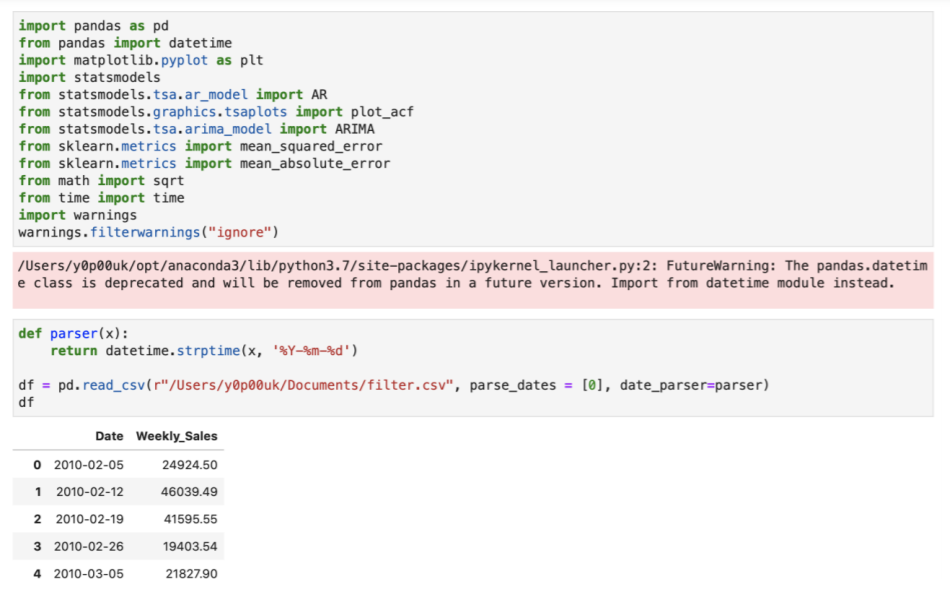
Reading the dataset
Now as we can see the date column is in month/date/year, the column name should be “ds” and Weekly sales should be “y”. So next step will be renaming the columns. This is one of the must step in FB Prophet forecasting.
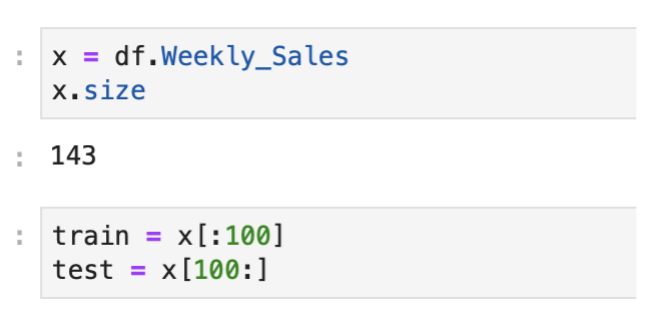
Splitting the data into train and test, so that we can train the model on training part and test the accuracy of the model on test data.
Now calling Prophet function and performing prediction
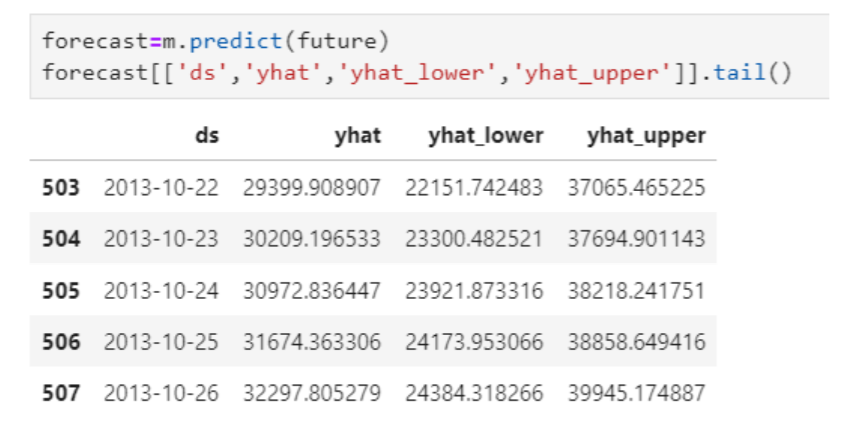
The yhat is the predicted value. Yhat_lower and yhat_upper is the prediction uncertainty interval.
Hence, for the error calculation we have to consider yhat.
Plotting the forecast:
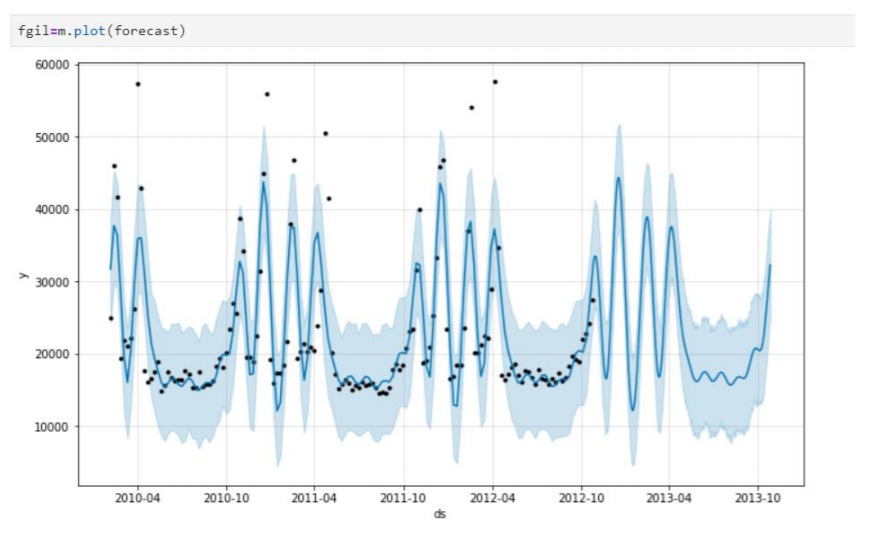
In the above graph, the blue line is the forecasted values and black dots are the actual values. We can see there are the black dot i.e the actual values are till October-2012 and as the model has forecasted for next year for which actual values are not available so, black dots are not present. From the above graph, the model seems to be captured the actual values quite well, without including holidays in the model.
Now, let’s include holidays in the model and see the difference.
Next step is to introduce the holidays, we have a number of holidays in a year. That we have to provide to the model, so that it can identify the trend of holidays every year.
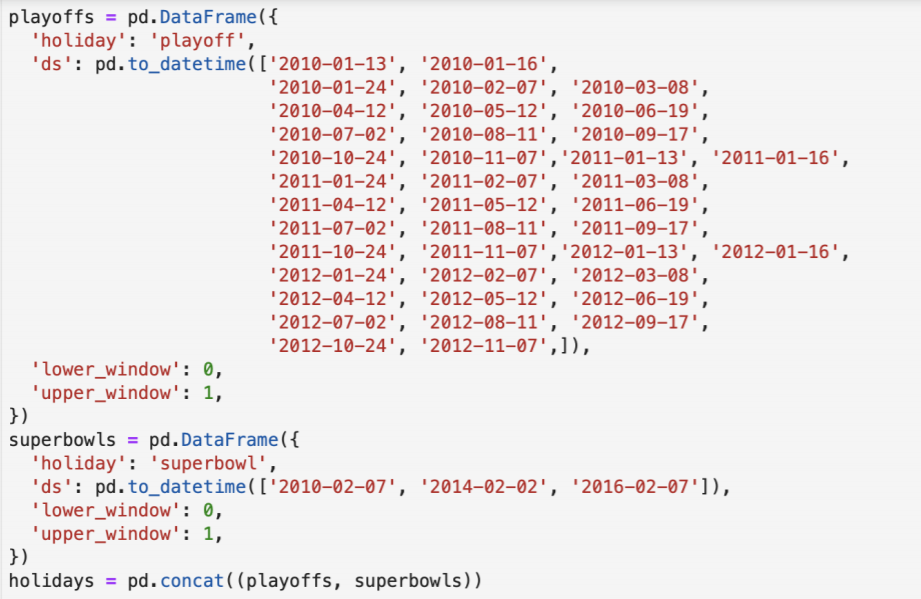
The above code lists out the dates of holidays (These are not the real holidays date of any country, I have considered some dates to make a list of holidays)
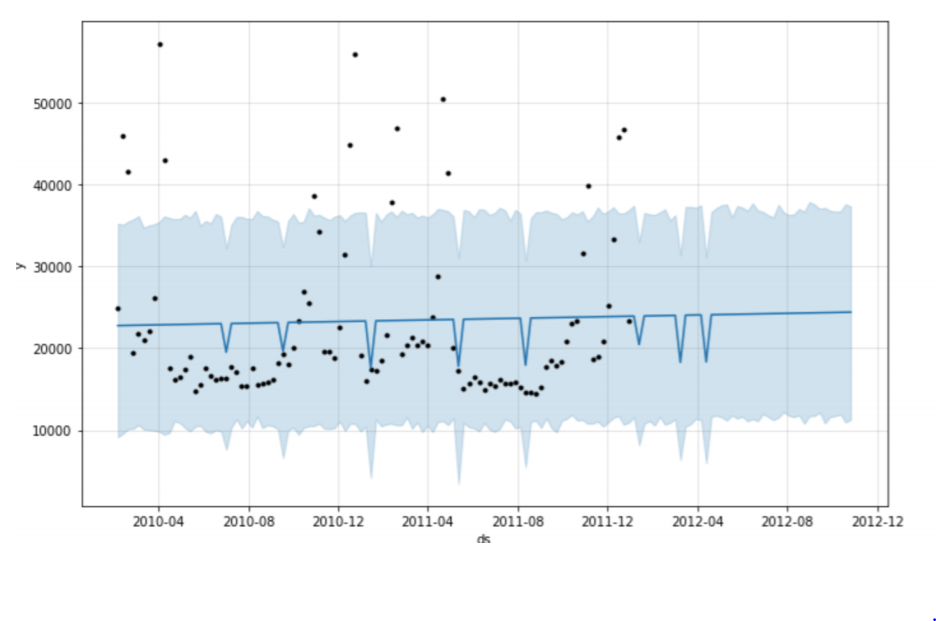
From the above graphs, we can see the model training is capturing the lows and highs in the data and based on that it is predicting for future.
Check the trend and seasonality component
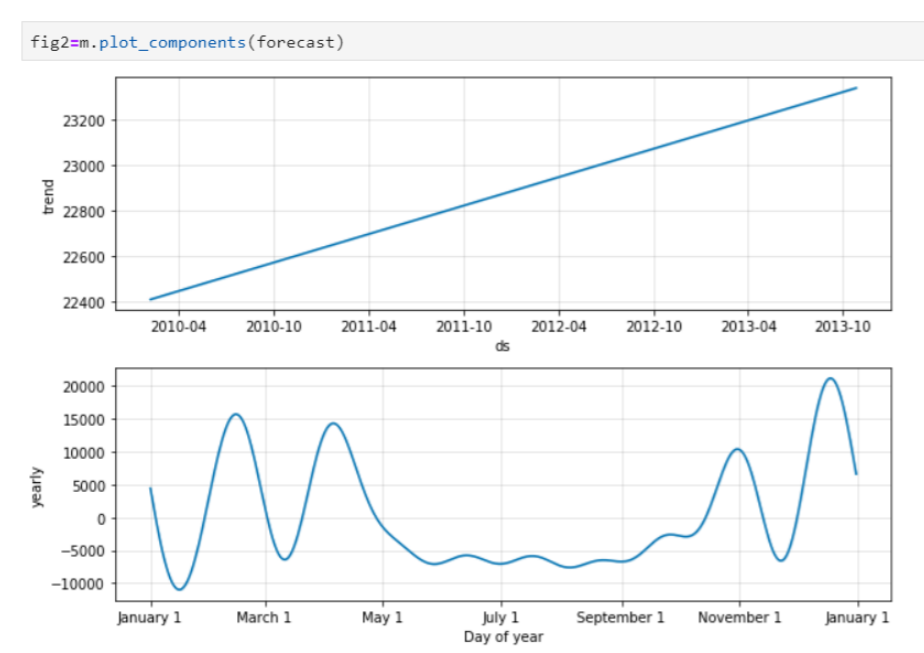
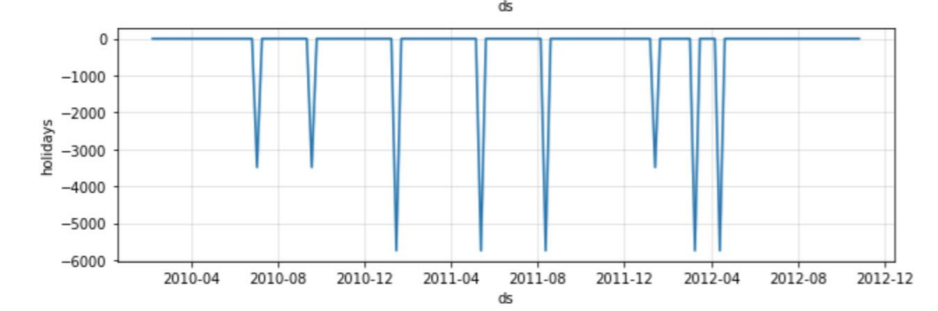
The model is also capturing the holidays year by year.
Calculating sMAPE error
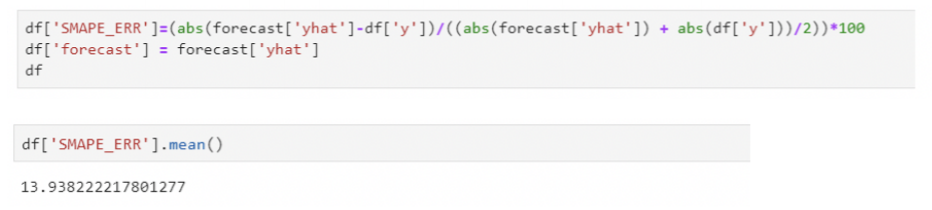
As, we can see that the sMAPE error mean is 13.93 %.
Now, let’s go through the ARIMA code:
Importing the libraries and data for model building. Ultimate goal is to calculate the sMAPE of
forecasted value.
Next, we have to split the data into train and test sets and trained the ARIMA model on train set. Once the model is trained, we can test the accuracy of the model using test set and calculating sMAPE value. Below code is splitting the data and training the model on train data.
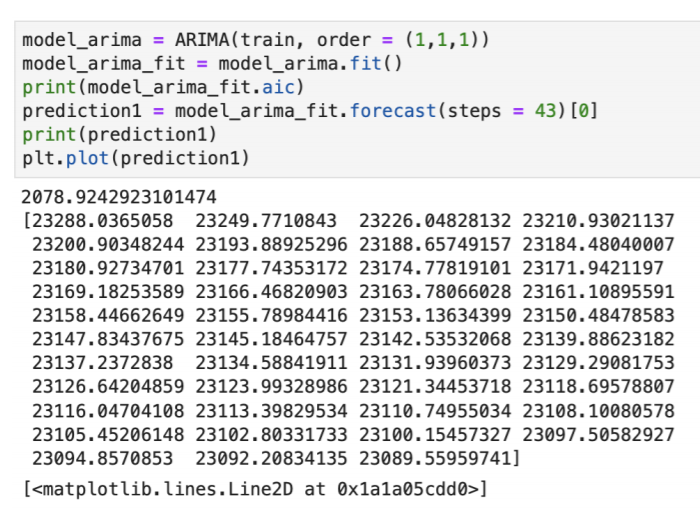
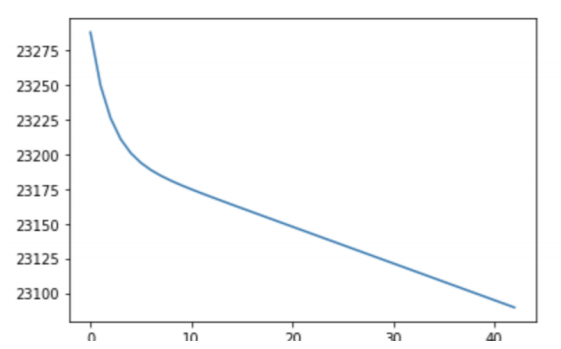
Calculating the sMAPE:
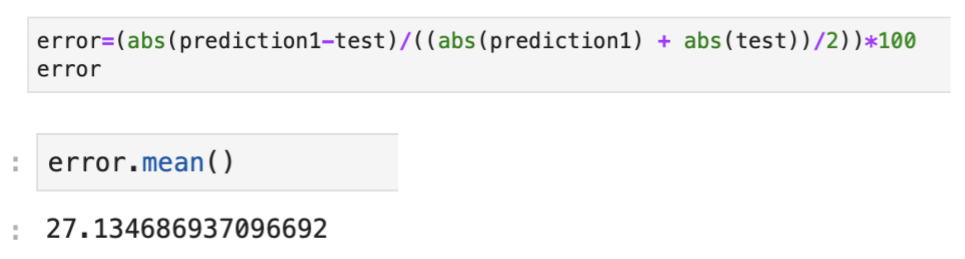
If we will do the forecasting using ARIMA with (1,1,1) grid, we will get sMAPE as 27.13% as
shown above. So, we can say that FBProphet is performing much better than ARIMA in this case. Although, there other criteria’s through which we can see the performance of the model and can make our judgements. But, for this paper, I am keeping our discussion limited to sMAPE criteria. As, we know that we can improve the model by hyper-tuning the parameters. Feel free play with parameters for better
result.
Any comment for improvement in the document is highly appreciated.
